Cylinder Volume Calculator - Enter radius and height and calculate the volume
Formula to Calculate Volume of a Cylinder
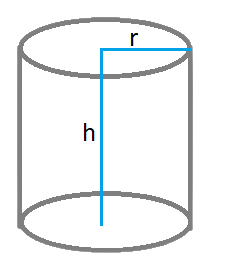
Calculate Volume of Solid Cylinder
Volume = π r² h
r is radius, h is height and Pi value is 3.14
Calculate Volume of a Cylinder with diameter
Volume = π d² h / 4
d is diameter, h is height and Pi value is 3.14
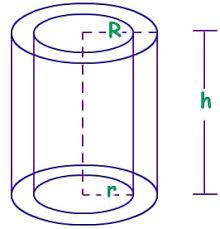
Calculate Volume of a Hollow Cylinder
Volume = π (R² - r²) h
R is outer radius, r is inner radius, h is height and Pi value is 3.14
Formula to Calculate Volume of a Sphere
Calculate Volume of a Sphere using Radius
Volume = 4/3 π r³
r is radius and Pi value is 3.14
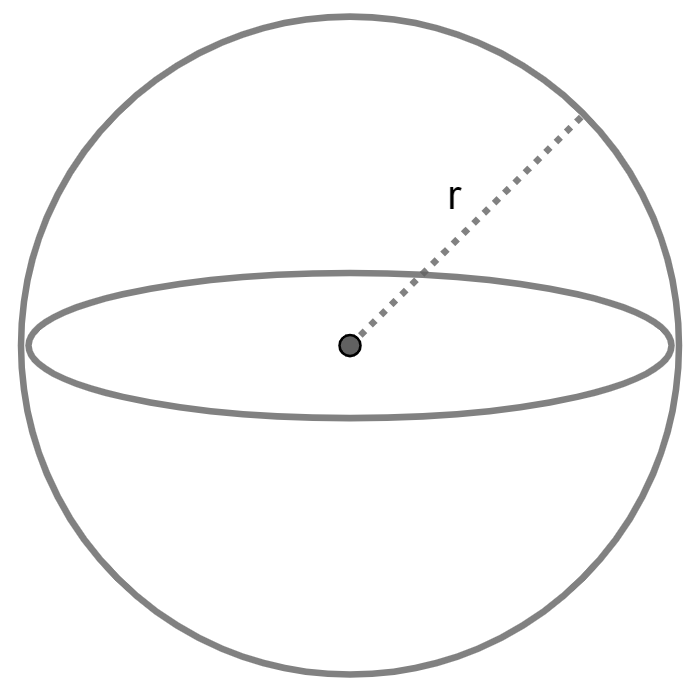
Calculate Radius of Sphere given the volume
Radius = (3V / 4π)⅓
V is volume and Pi value is 3.14
Formula to Calculate Volume of a Hemisphere
Calculate Volume of Hemisphere using Radius
Volume = 2/3 π r³
r is radius and Pi value is 3.14
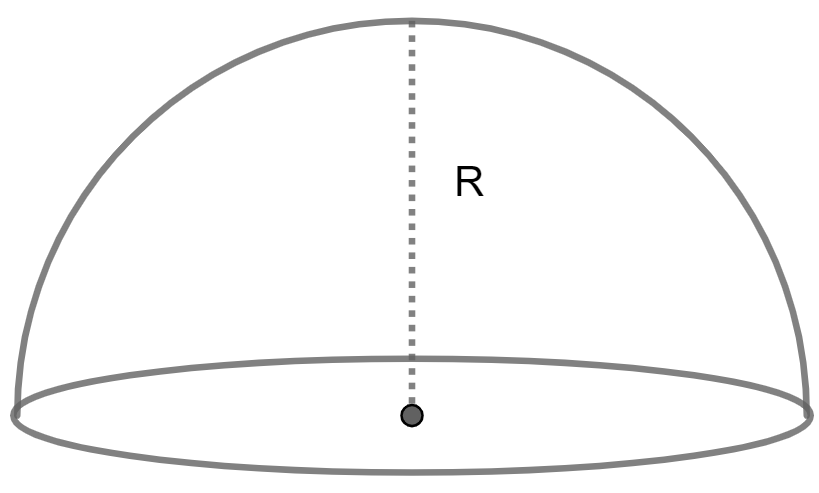
Find the radius of a Hemisphere given its volume
Radius = (3V / 2π)⅓
V is volume and Pi value is 3.14
Formula to Calculate Volume of a Cone
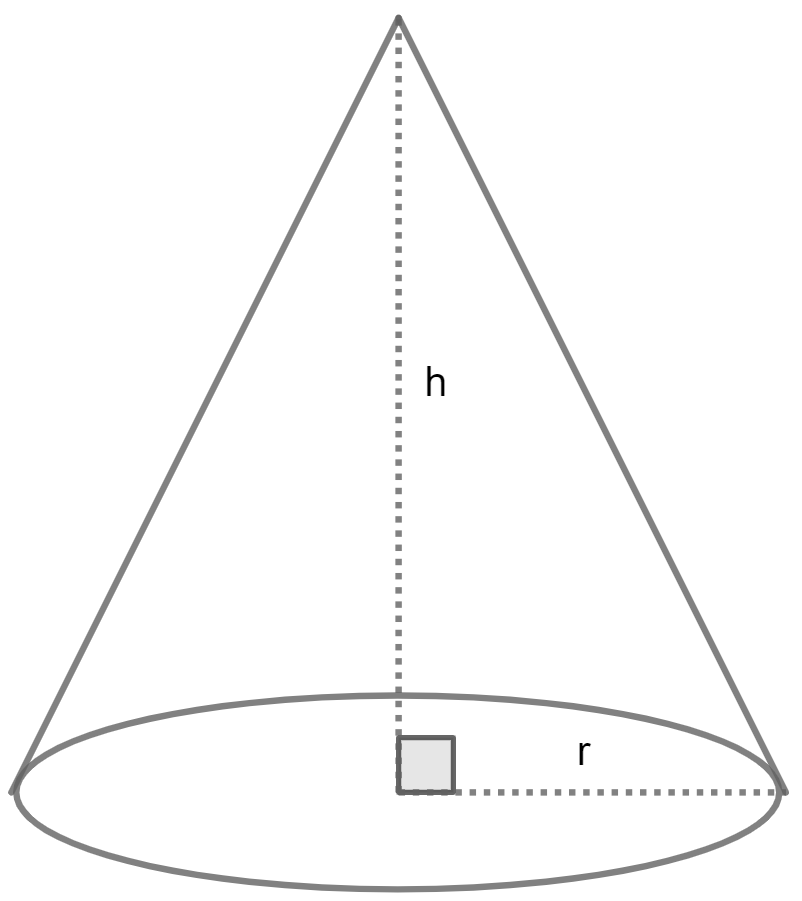
Calculate Volume of a Cone
Volume = 1/3 h π r²
r is radius, h is height and Pi value is 3.14
Formula to Calculate Volume of a Cube
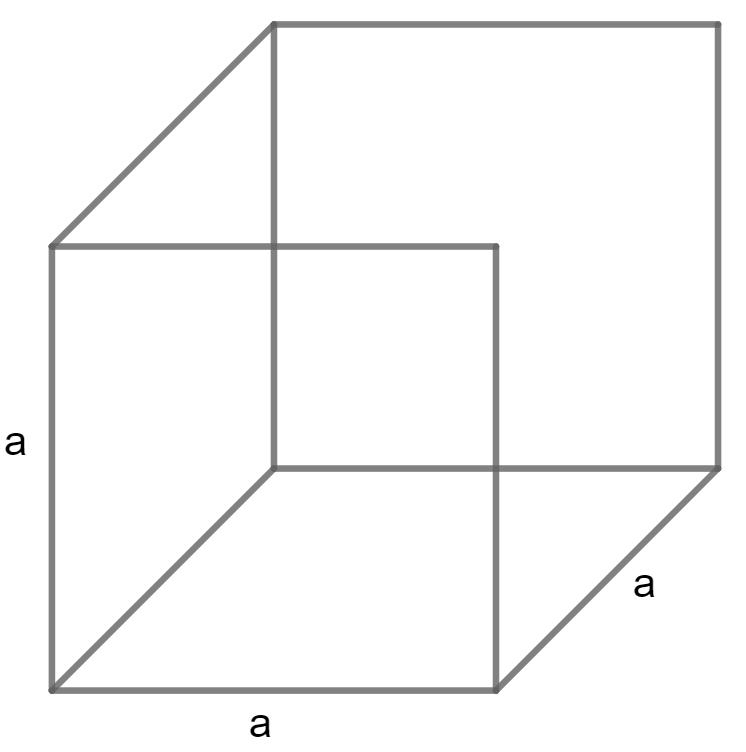
Calculate Volume of Cube using its Edge
Volume = a³
a is edge
Find the Edge of a Cube for a given Volume
Edge = (V)⅓
V is volume
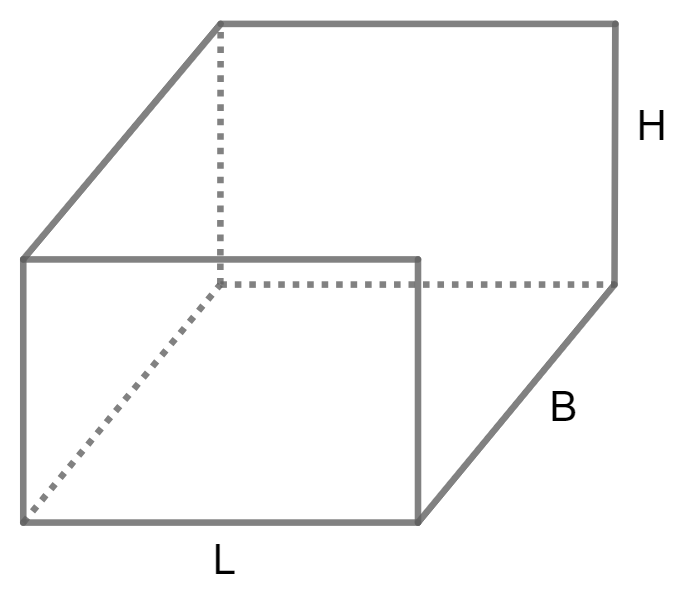
Formula to Calculate Volume of a Cuboid
Calculate Volume of Cuboid using Length, Width and Height
Volume = L * W * H
L is Length, W is Width, and H is Height
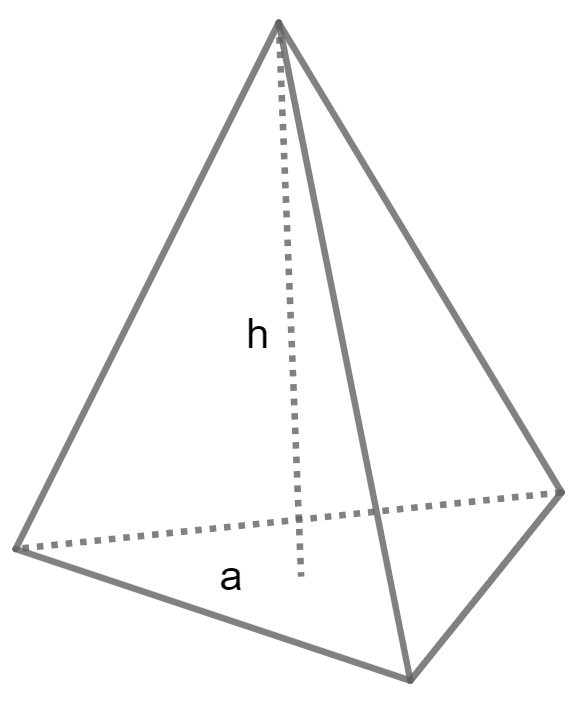
Formula to Calculate Volume of a Pyramid
Calculate Volume of Triangular Pyramid using Area and Height
Volume = 1/3 A H
A is Area and H is Height
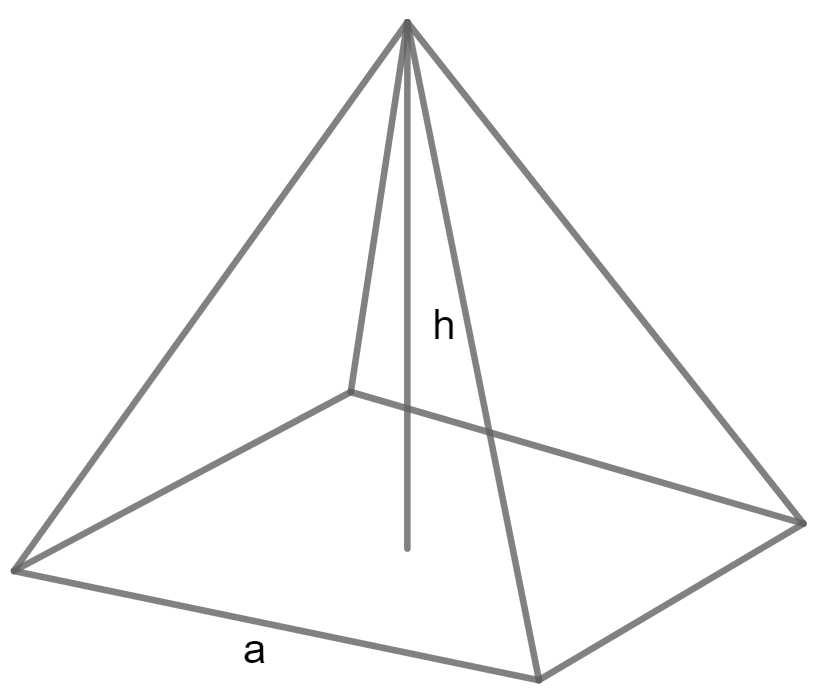
Calculate Volume of a Square Pyramid using Base edge and Height
Volume = a² h/3
A is base edge and H is Height
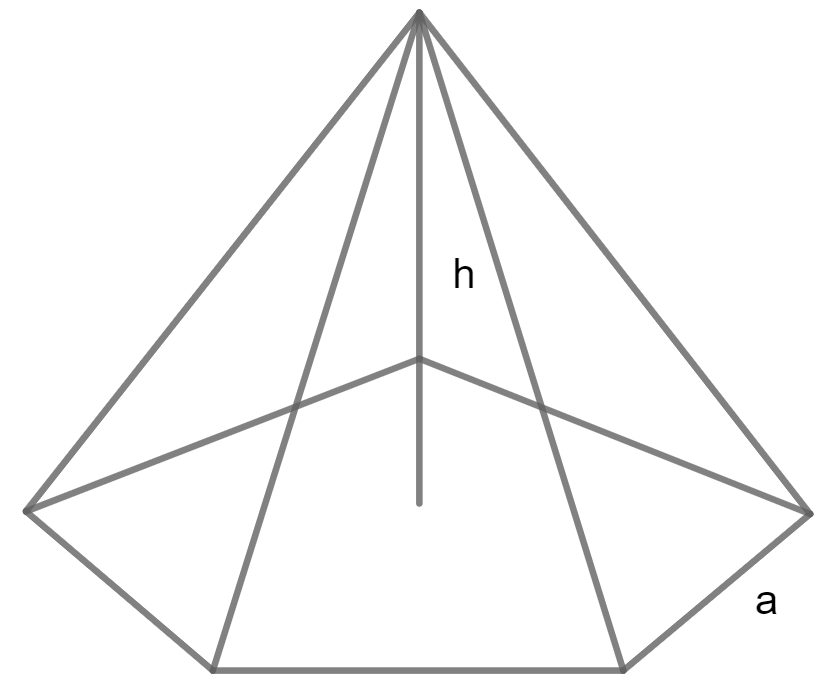
Calculate Volume of Pentagonal Pyramid using Base edge and Height
Volume = 5/12 tan(54°)h a²
A is base edge and H is Height
Calculate Volume of a Rectangular Pyramid using Base length, Width and Height
Volume = l w h / 3
L is base length, W is Width and H is Height
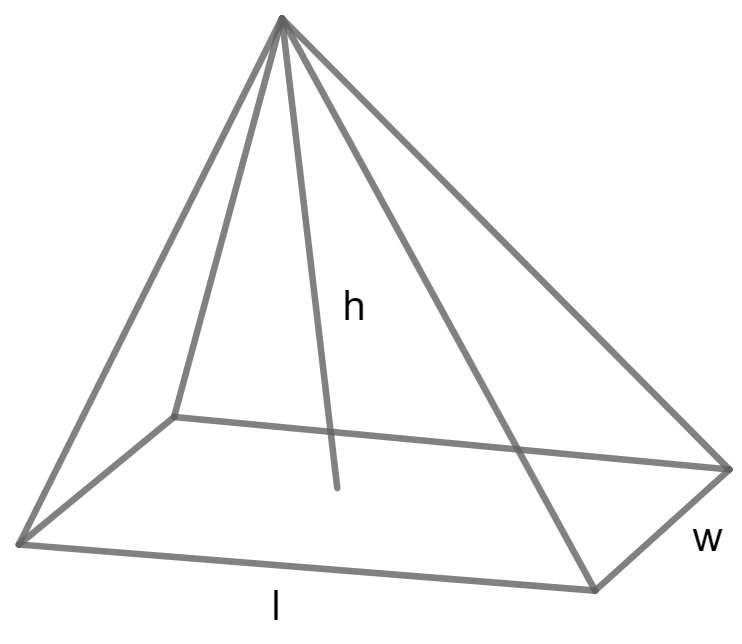
Formula to Calculate Volume of a Prism
Calculate Volume of a Triangular using Base Edge, Length and Height
Volume = 1/2 a h l
A is Base edge and H is Height and L is Length
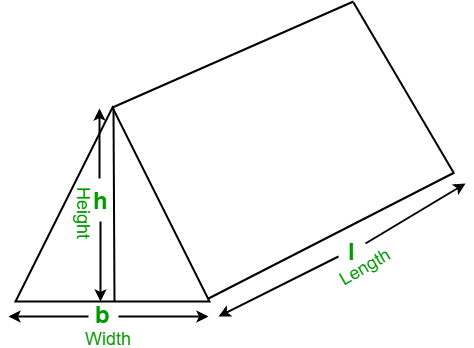
Calculate Volume of a Square Prism using Base edge and Height
Volume = a² h
A is base edge and H is Height
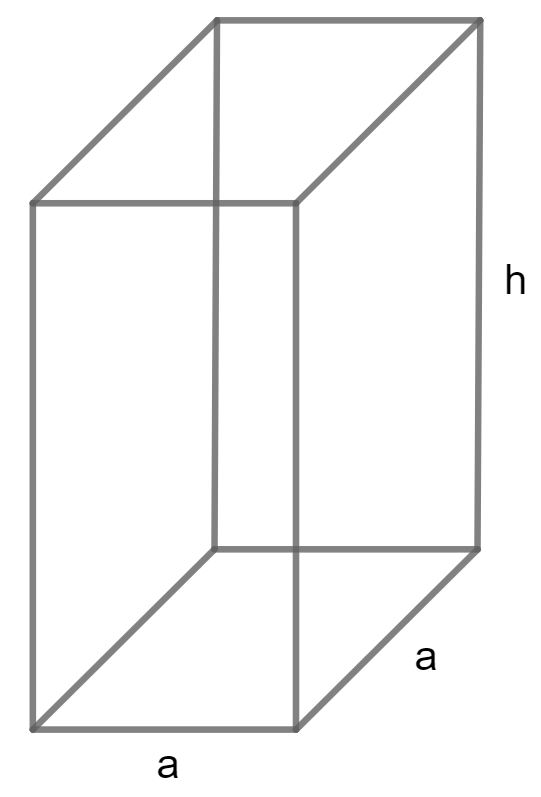
Calculate Volume of a Rectangular Prism using Width, Length and Height
Volume = w l h
W is Width and L is Length and H is Height
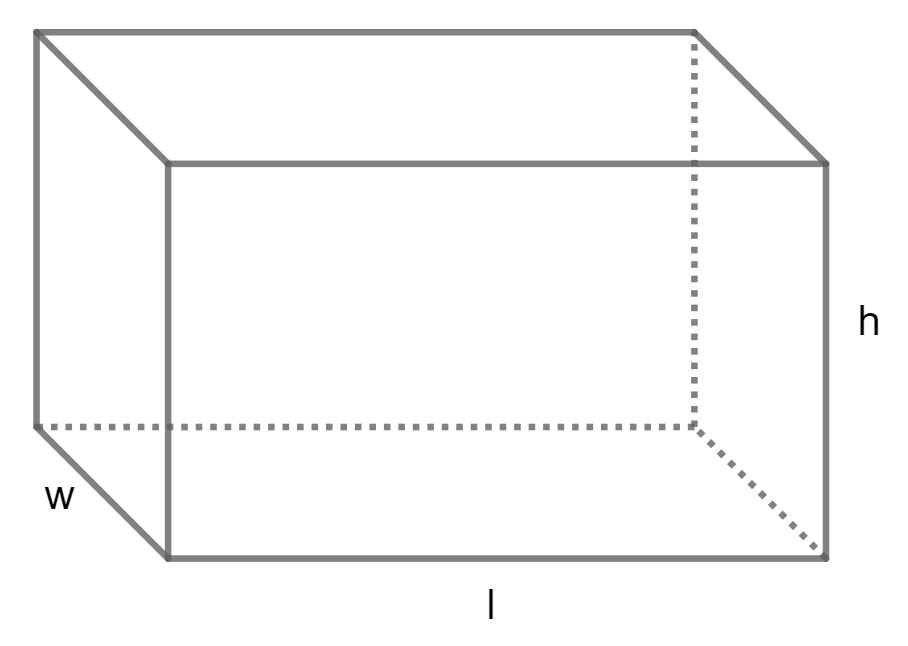
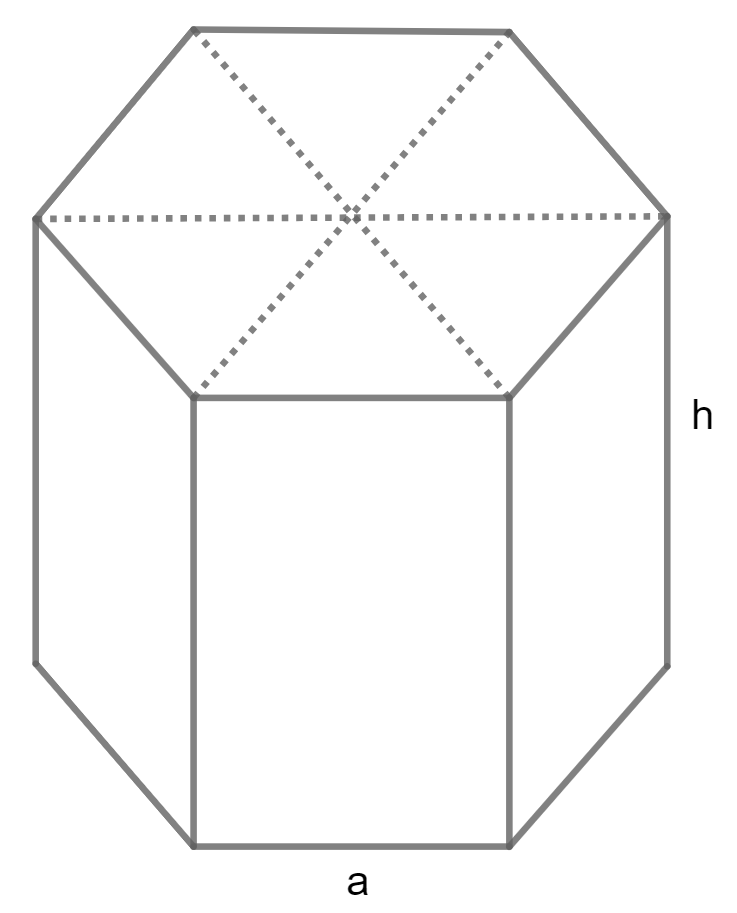
Calculate Volume of a Pentagonal using Base edge and Height
Volume = (1 / 4) * square root(5 * (5 + 2 * square root(5))) a² h
A is base edge and H is Height
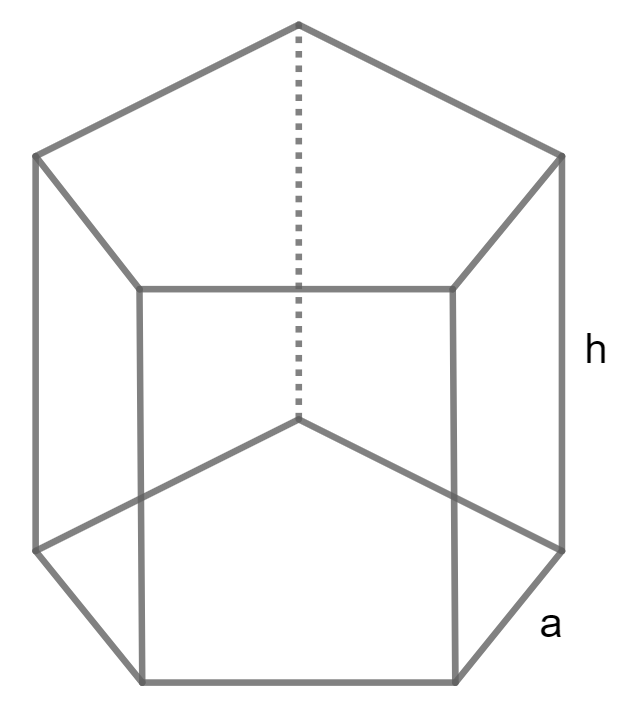
Calculate Volume of a Hexagonal using Base edge and Height
Volume = (3 * square root(3) / 2) a² h
A is base edge and H is Height
Formula to Calculate Volume of an Ellipsoid
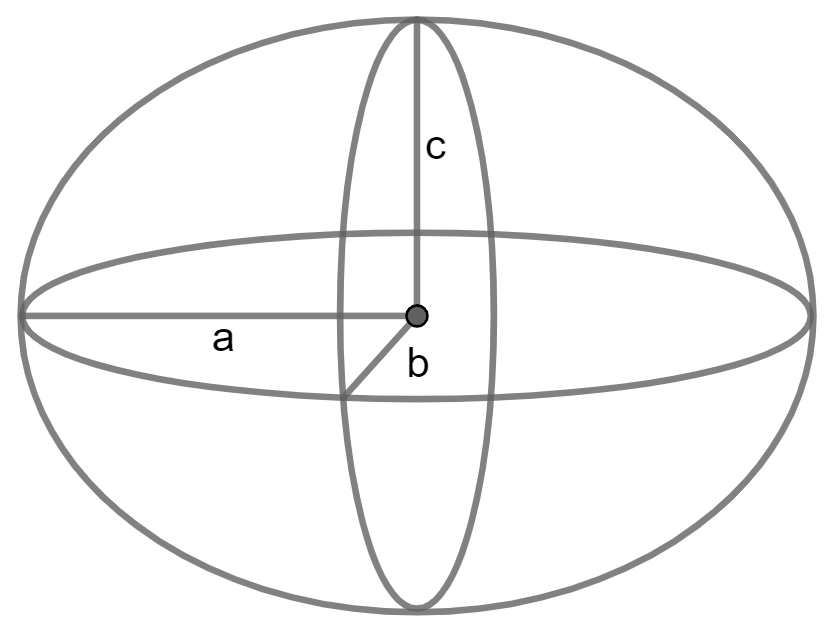
Calculate Volume of a Ellipsoid using Axes
Volume = 4/3 π a b c
A, B and C are axes
Formula to Calculate Volume of a Tetrahedron
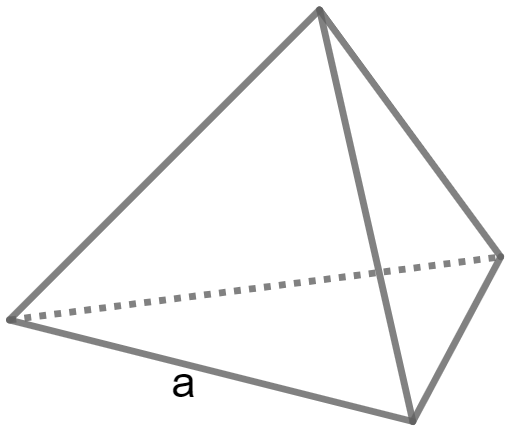
Calculate Volume of a Tetrahedron using its Edge
Volume = a³ / 6 * square root(2)
A is Edge
Calculate Edge of a Tetrahedron using Volume
Edge = square root(2) * (3 * V)⅓
V is Volume
Formula To Calculate Volume of a Hollow Cylinder
Calculate Volume of a Hollow Cylinder using radius and height
Volume = π (R² - r²) h
R is outer radius, r is inner radius, h is height and Pi value is 3.14

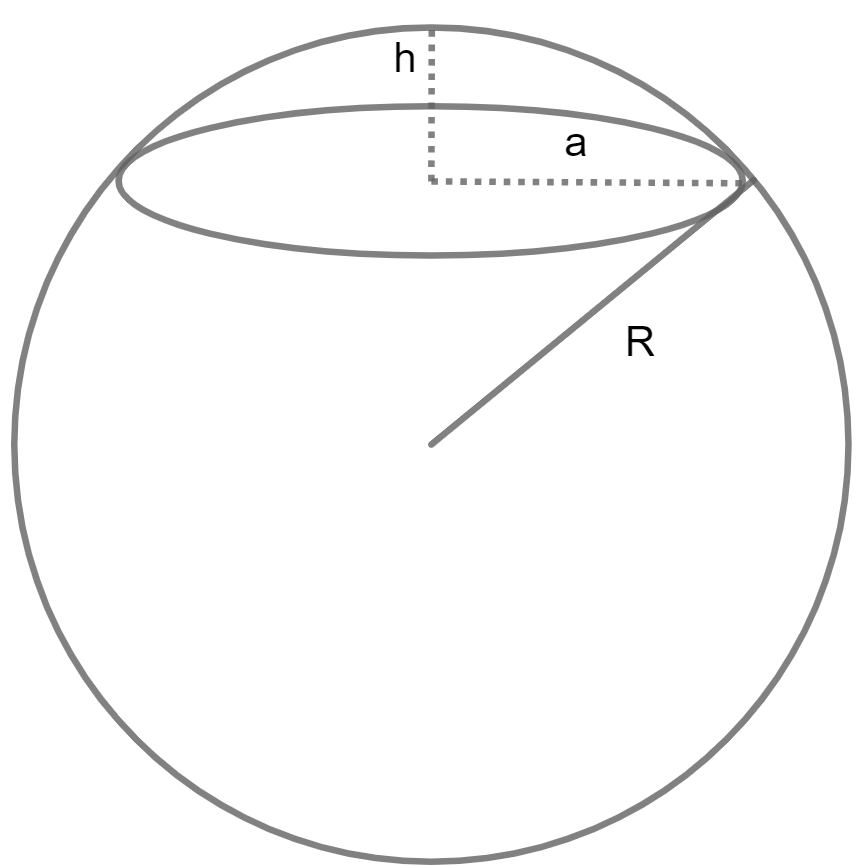
Formula to Calculate Volume of a Spherical Cap
Calculate Volume of a Spherical Cap using Radius and Height
Volume = (1/3) π h² (3R - h)
H is Height, R is Radius and Pi value is 3.14