Radians to Degrees Conversion Calculator
Convert Radians to Degrees (rad to deg) or Degrees to Radians (deg to rad)
Enter either radian or degree and calculate the equivalent
=
Formula to convert between Radians and Degrees
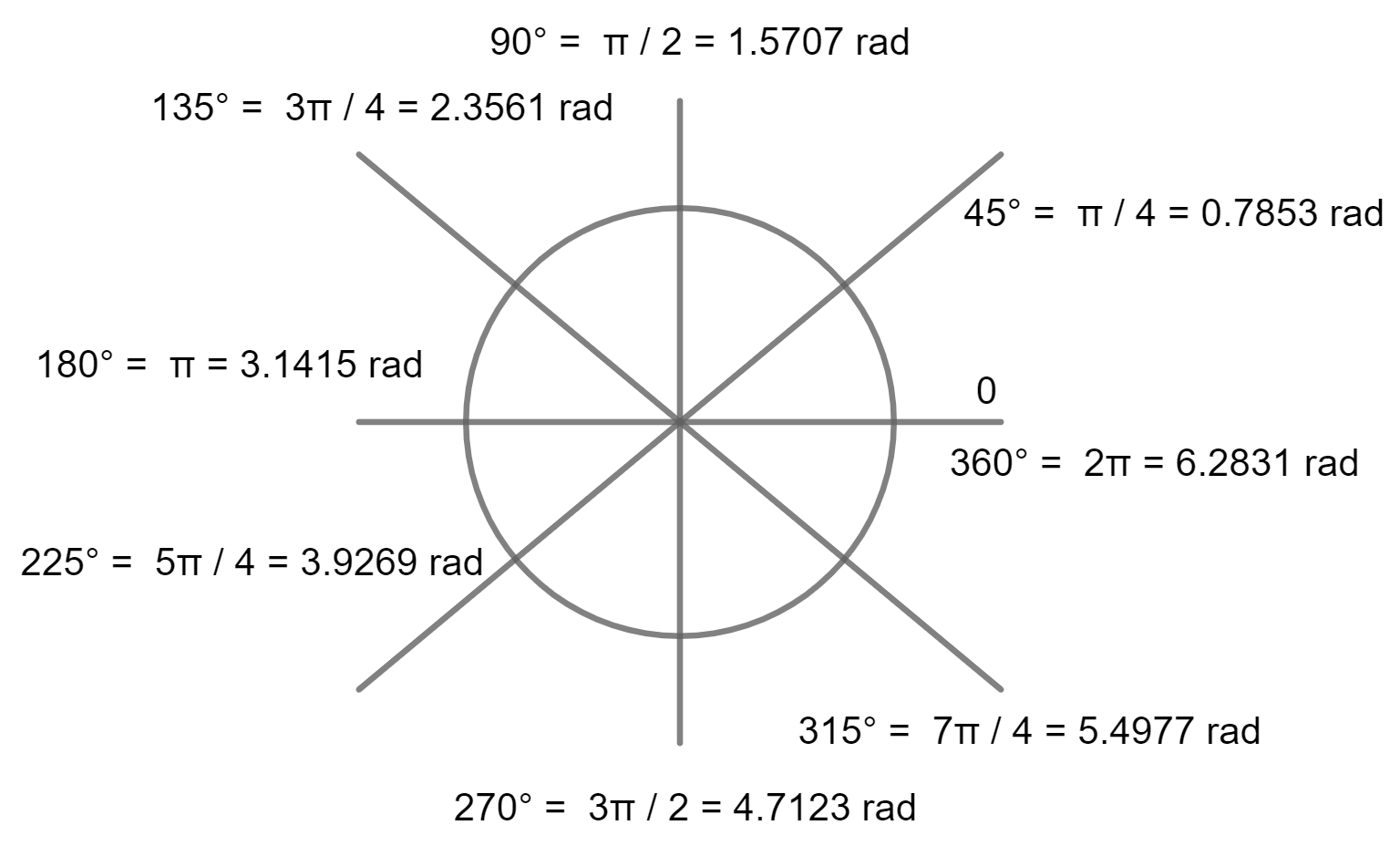
How many Radians to Degrees?
rad = π/180 * degree = 0.0174 * degrees, where π = 3.14
For example, to convert 90 degrees to radians, multiply degrees by π/180
radians = π/180 * 90 = 0.0174 * 90 = 1.57 radians
How many Degrees in a Radian?
- To convert radian to degrees, multiple radian value with 180 / π
- Therefore, 0.5 radians = 28.65 degrees.
degree = 180 / π * radians = 57.32 * radians, where π = 3.14
For example, to convert 0.5 radians to degrees:
degrees = 180 / π * 0.5 = 57.32 * 0.5 = 28.65 degrees
What are Radians and Degrees?
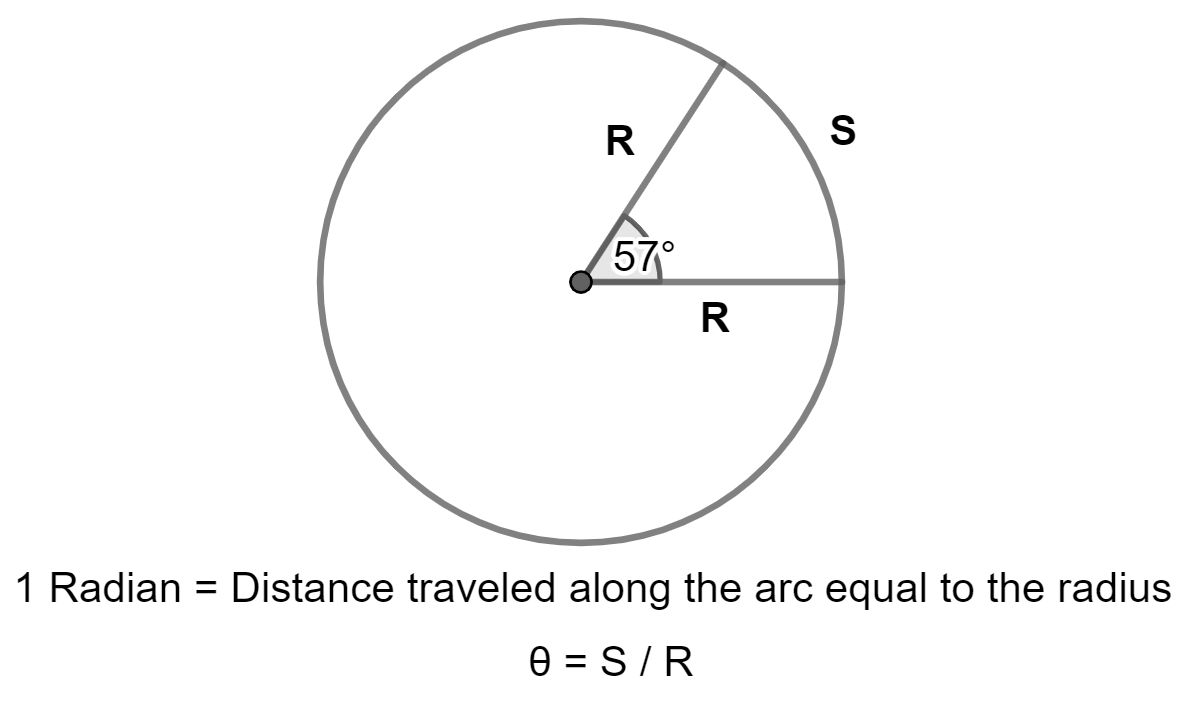
- Radians and Degrees are units of measurement of an angle. The SI Unit of an angle is 'Radians'.
- A radian is defined as the angle subtended at the center of a circle by an arc whose length is equal to the radius of the circle.
- A degree is defined as the angle subtended at the center of a circle by an arc whose length is equal to 1/360th of the circumference of the circle. The full circle is 360 degrees
- A radian is a bigger unit than a degree. 1 radian is equal to 57.2958 degrees.
- Symbol of a degree is 'θ'. Symbol of a Radian is 'rad'
- Degrees are simpler and easy to visualize with a circle of 360 degrees. Degrees are used in any exterior activities such as surveying, construction work, drawing arcs and circles on paper using protractor and in maps and clocks
- Radians are more precise than degrees and used in calculations such as in trignometry, physics angular and rotational motion.
How is Pi related to Radians and Degrees?
- The ratio of Circumference of a Circle to the Diameter (C/D) is a fixed value and it is always equal to 22/7 which is 3.14159. This fixed value for C/D = 3.141 holds good for any type of circle
- This ratio is defined as Pi represented by the symbol π which represents the value 3.14.
- We know that the diameter of any circle is twice of the radius.
Therefore, Circumference/Diameter = Circumference/(2 * Radius) = π - Circumference = 2* π * Radius = 2πR
- As we know a Radian is defined as the angle formed by the arc of a circle with the radius.
A circumference is a full arc of 360 degrees. Therefore, radian of a full circle = circumference/radius = 2*π = 2 * 3.14 = 6.14 radians - The angle formed by the full circle is 360 degrees. Therefore 360 degrees = 2π radians. which forms the basis for the conversion between the 2 units
Degrees to Radians Table
| Angle in Degree (deg) | In Radians (rad) |
|---|---|
| 1 degree | 0.017 rad |
| 2 degrees | 0.034 rad |
| 5 degrees | 0.087 rad |
| 10 degrees | 0.174 rad |
| 30 degrees | 0.523 rad |
| 45 degrees | 0.785 rad |
| 57.3 degrees | 1 rad |
| 60 degrees | 1.047 rad |
| 90 degrees | 1.57 rad |
| 135 degrees | 2.3561 rad |
| 180 degrees | 3.14 rad |
| 240 degrees | 4.2 rad |
| 270 degrees | 4.71 rad |
| 360 degrees | 6.28 rad |
| 450 degrees | 7.85 rad |
| 540 degrees | 9.42 rad |
| 630 degrees | 10.99 rad |
| 720 degrees | 12.56 rad |
| 810 degrees | 14.13 rad |
| 900 degrees | 15.7 rad |
| 990 degrees | 17.27 rad |
| 1080 degrees | 18.84 rad |
| 1170 degrees | 20.42 rad |
| 1260 degrees | 21.99 rad |
| 1350 degrees | 23.56 rad |
| 1440 degrees | 25.13 rad |
| 1530 degrees | 26.7 rad |
| 1620 degrees | 28.27 rad |
| 1710 degrees | 29.84 rad |
| 1800 degrees | 31.41 rad |
| 1890 degrees | 32.98 rad |
| 1980 degrees | 34.55 rad |
| 2070 degrees | 36.12 rad |
| 2160 degrees | 37.69 rad |
| 2250 degrees | 39.26 rad |
| 2340 degrees | 40.84 rad |
| 2430 degrees | 42.41 rad |
| 2520 degrees | 43.98 rad |
| 2610 degrees | 45.55 rad |
| 2700 degrees | 47.12 rad |
| 2790 degrees | 48.69 rad |
| 2880 degrees | 50.26 rad |
| 2970 degrees | 51.83 rad |
| 3060 degrees | 53.4 rad |
| 3150 degrees | 54.977 rad |
| 3240 degrees | 56.54 rad |
| 3330 degrees | 58.11 rad |
| 3420 degrees | 59.69 rad |
| 3510 degrees | 54.97 rad |
| 3600 degrees | 62.83 rad |
Radians to Degrees Table
| Pi Radians (rad) | In Degrees (deg) |
|---|---|
| Quarter Pi / 0.25 rad | 45 degrees |
| Half Pi / 0.5 rad | 90 degrees (Quarter Circle) |
| 1 rad | 180 degrees (Half Circle) |
| 2 rad | 360 degrees (One Circle) |
| 3 rad | 540 degrees (One and Half Circle) |
| 4 rad | 720 degrees (Two Circle) |
| 5 rad | 900 degrees (Two and Half Circle) |
| 6 rad | 1080 degrees (Three Circle) |
| 7 rad | 1260 degrees (Three and Half Circle) |
| 8 rad | 1440 degrees (Four Circle) |
| 9 rad | 1620 degrees (Four and Half Circle) |
| 10 rad | 1800 degrees (Five Circle) |
FAQ on Rad-Degree conversions
What is meant by circle degrees?
1 circle = 360 degrees.
A circle multiplied by 360 gives the angle in degrees.
2 circle = 720 degrees.
10 circle = 3600 degrees.
How many radians in a circle?
6.28 radians
What is pi radians to degrees?
pi radians is 180 degrees
2 pi radians is 360 degrees
What is a unit circle?
The unit circle is a circle with a radius of 1 unit.
An angle of 1 radian subtends an arc length of 1 unit on the unit circle.
This makes the unit circle a convenient tool for visualizing angles in radians.
What is the radian of a unit circle?
Since Unit circle is a circle of radius = 1 unit.
It is 2 Pi or 6.28 radians.
A degree is a unit of measurement of an angle.
One rotation around a circle is equal to 360 degrees.
What is theta and is it in degrees or radians?
Theta (θ) is simply a variable to indicate an angle and is typically used in mathematical equations.
It can be represented in radians or in degrees.
What is meant by pi over 3?
It is 1.0471 rad which means 60 degrees
