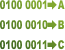Hex to Binary - Binary to Hex Converter
Convert Hexadecimal to Binary or Binary to Hexadecimal
You can input in any of the fields and get equivalent values.
How to convert Hex to Binary?
In hex system, the numbering is from 0 to 9, A to F representing upto 15.
In binary system, we can represent each hex with 4 bits ranging from 0000 (0 in hex) to 1111(A in hex)
Take every hex digit and represent it by its binary equivalent and discard the leading zeroes.
For eg, to convert 1FA7 to binary ,take each hex and convert to binary 1- 0001 F- 1111 A - 1010 7 - 0111 1FA7 to binary = 1111110100111
1FA7 hex to binary is equal to 1111110100111
How to convert Binary to Hex?
Take 4 bits starting from left to right (LSB) and convert to its equivalent hex value and keep repeating.
Eg if the binary value is 111011 , take the last 4 bits 1011, this maps to B in hex (11 in decimal) The remaining 2 bits are 11 which is 3 in hex. Concatenate them to get the hex value.
01 1011 in binary is 3B in hex
Hex to Binary Converter - Binary to Hexadecimal table
| Hexadecimal | Binary | Decimal |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 10 | 2 |
| 3 | 11 | 3 |
| 4 | 100 | 4 |
| 5 | 101 | 5 |
| 6 | 110 | 6 |
| 7 | 111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| A | 1010 | 10 |
| B | 1011 | 11 |
| C | 1100 | 12 |
| D | 1101 | 13 |
| E | 1110 | 14 |
| F | 1111 | 15 |
| 18 | 11000 | 24 |
| 19 | 11001 | 25 |
| 1A | 11010 | 26 |
| 1B | 11011 | 27 |
| 1C | 11100 | 28 |
| 1D | 11101 | 29 |
| 1E | 11110 | 30 |
| 20 | 100000 | 32 |
| 30 | 110000 | 48 |
| 32 | 110010 | 50 |
| 38 | 111000 | 56 |
| 40 | 1000000 | 64 |
| 80 | 10000000 | 128 |
| 100 | 100000000 | 256 |
| 200 | 1000000000 | 512 |
| 400 | 10000000000 | 1024 |
| 800 | 100000000000 | 2048 |
Frequently Asked Questions on Binary to Hexadecimal converter
Hexadecimal is a numbering system which having 16 as base.
It is used to represent large numbers.
This number system is also called as base-16.
Mainly used in computers to reduce large string of binary to four digits to understand easily.
Binary is number system having two values as 0 and 1 Digits(0 and 1) in this system is called bit.
Used to represent two possible states ON/Off as 0 and 1
