LCM - Least Common Multiple
Find the lowest common multiple of numbers. Learn about lcm by division method, lcm by prime factorization method and lcm by grid method
You can input in any of the fields and get equivalent values.
=
=
Least Common Multiple : 2
What is LCM?
- Least Common Multiple(LCM)
- What Methods are there to find LCM
- Long Division Method
- Prime Factorization Method
- Grid Method
- Cake Method (Ladder Method)
- Box Method
- Listing Multiples Method
Least common multiple of any group of numbers is defined as the smallest number that will be the multiple of all the numbers in a group.
A multiple of a number is obtained by multiplying the number with any other number (which is an integer, whole number or 0) for eg, 5, 10, 15, 20 , 25 ,30 are multiples of 5.
How to find the least common factor of 2 or more numbers?
LCM By Listing Multiples Method
- Step 1: List few multiples of each numbers separately.
- Step 2: Collect the first common multiple of two numbers.
- Step 3: First and smallest common multiple of two number is the LCM of the numbers.
LCM by division method
- Step 1: Write the numbers in a line separated by comma.
- Step 2: start to divide the number by prime numbers and write the quotient in the next line.
- step 3: Repeat the process of dividing numbers by prime numbers untill you get 1 in the last row.
- Step 4: LCM of the two numbers will be the product of all prime numbers used in the long division.
Examples: LCM of 12 and 24
- Step 1: List the few multiples of 12 and 24. Multiples of 12 is 12 , 24 ,36,...
Multiples of 24 is 24 , 48 , 72,... - Step 2: First common multiple of 12 and 24 is 24.
- Step 3: So the Least Common Multiple is 24.
LCM by Long Division method (LCM example of 12, 24, 45)
- Step 1: Write the 12 ,24 and 45 numbers in the same line.
- Step 2: Divide all the number by 3 write the quotient 4 , 8 ,15 in the next line.Repeat the process now divide the numbers by 2, since 15 is not divisible by 2 take down 15 to next line as it is.
So we will get 2 , 4 , 15 in the next line.
Again divide the numbers by 2 we get 1 , 2 , 15 and next divide by 2 we get 1 , 1, 15.Now divide by 3 to make 15 to become 1. So in the next line 1, 1, 5 now divide the whole by 5 now the result will be 1, 1, 1. - Step 3: Now multiply all prime numbers in the Long division method 2 x 2 x 2 x 3 x 3 x 5 = 360. So the LCM of 12 , 24 and 45 is 360.
- Long division Flow
LCM by Prime Factorization method
- Step 1: Write down the prime factorization of each number
- Step 2: Now take the common factors and take the remaining factor and multiply the factors.
- Step 3: Multiplication of the factors will be the lcm of the numbers.
- Example: LCM of 12 and 24 using Prime factorization method.
Prime factorization of 12 = 2 x 2 x 3,
Prime factorization of 24 = 2 x 2 x 2 x 3
we have 2 , 2 and 3 as common factor take these factors and we have one more 2 which is not a common factor take this too.
Multiply 2 x 2 x 3 x 2 this will be the lcm of 12 and 24.
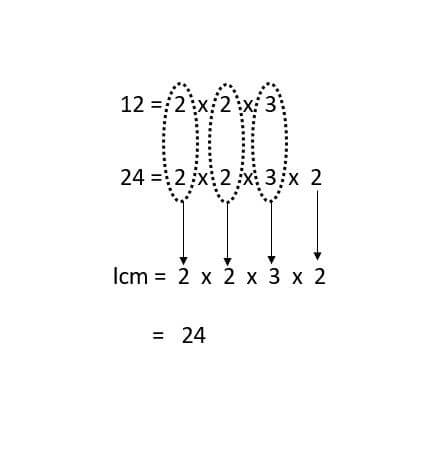
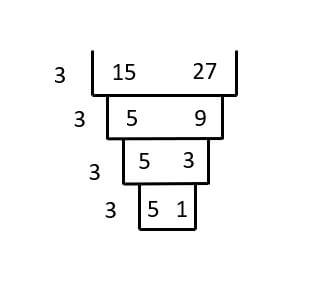
LCM By Cake Method / LCM By Ladder Method
- Step 1: This method is the one of the easiest way to find the lcm of the numbers. Write down the number in the first layer.(layer looks like top of the cake |__|.)
- Step 2: Divide the Layer numbers by prime numbers and write the result in the next Layer.If any number in the layer is not divisible then take it down as it is.
- Step 3: Continue dividing the cake layers untill you get only prime numbers in the last layer.
LCM is the product of the numbers in the left side of the layers and the last layer. - Example: LCM of 15 and 27
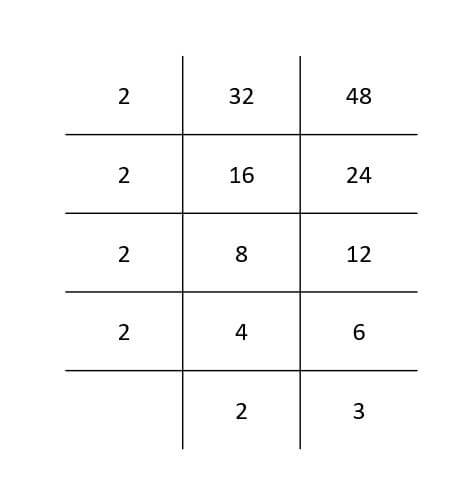
LCM By Grid Method
- Step 1: Write down the number separated by vertical line and horizontal line to separate each grid.
- Step 2: Divide the numbers by prime number and write the result in the next row grid.If any number in the upper grid is not divisible then take it down as it is.
- Step 3: Continue dividing the numbers untill you get only prime numbers in the last layer.
Product of the prime numbers will be the LCM of the numbers. - Example: LCM of 32 and 48
LCM By Box Method
- Step 1: Write down the number separated by vertical line and horizontal line.
- Step 2: Divide the numbers by prime number and write the result in the next line.If any number is not divisible then take it down as it is.
- Step 3: Continue dividing the numbers untill you get only prime numbers.
Product of the prime numbers will be the LCM of the numbers.
Lowest Common Multiple (LCM) Table
| What is the LCM of | LCM is |
|---|---|
| 8 and 12 | 24 |
| 6 and 8 | 24 |
| 6 and 9 | 18 |
| 9 and 12 | 36 |
| 4 and 6 | 12 |
| 8 and 10 | 40 |
| 6 and 10 | 30 |
| 9 and 15 | 45 |
| 4 and 10 | 20 |
| 12 and 18 | 36 |
| 12 and 15 | 60 |
| 3 and 5 | 15 |
| 3 and 8 | 24 |
| 3 and 4 | 12 |
| 4 and 8 | 8 |
| 7 and 8 | 56 |
| 5 and 6 | 30 |
| 7 and 9 | 63 |
| 10 and 12 | 60 |
| 8 and 9 | 72 |
| 6 and 7 | 42 |
| 3 and 7 | 21 |
| 4 and 7 | 28 |
| 12 and 16 | 48 |
| 4 and 5 | 20 |
| 5 and 7 | 35 |
| 6 and 12 | 12 |
| 3 and 9 | 9 |
| 4 and 9 | 36 |
| 6 and 15 | 30 |
| 5 and 7 | 35 |
| 4 and 5 | 20 |
| 10 and 15 | 30 |
| 15 and 20 | 60 |
| 16 and 24 | 48 |
| 2 and 3 | 6 |
| 18 and 24 | 72 |
| 5 and 10 | 10 |
| 3 and 6 | 6 |
| 4 and 12 | 12 |
| 12 and 20 | 60 |
| 2 and 5 | 10 |
| 2 and 6 | 6 |
| 24 and 36 | 72 |
| 15 and 25 | 75 |
| 5 and 8 | 40 |
| 14 and 21 | 42 |
| 12 and 30 | 60 |
| 5 and 9 | 45 |
| 6 and 14 | 42 |
| 12 and 5 | 60 |
| 7 and 12 | 84 |
| 2 and 4 | 4 |
| 16 and 20 | 80 |
| 5 and 15 | 15 |
| 8 and 14 | 56 |
| 8 and 20 | 40 |
| 4 and 14 | 28 |
| 2 and 7 | 14 |
| 18 and 27 | 54 |
| 15 and 18 | 90 |
| 2 and 9 | 18 |
| 20 and 30 | 60 |
| 24 and 30 | 120 |
| 18 and 30 | 90 |
| 3,4 and 5 | 60 |
| 2 and 8 | 8 |
| 8 and 5 | 40 |
| 12 and 14 | 84 |
| 7 and 14 | 98 |
| 6 and 18 | 18 |
| 3 and 12 | 12 |
| 4 and 16 | 16 |
| 10 and 14 | 70 |
| 3 and 10 | 30 |
| 5 and 11 | 55 |
| 11 and 12 | 132 |
| 24 and 32 | 96 |
| 5 and 20 | 20 |
| 10 and 25 | 50 |
| 2,3 and 5 | 30 |
| 7 and 11 | 77 |
| 6 and 16 | 48 |
| 8 and 15 | 120 |
| 9 and 10 | 90 |
| 9 and 24 | 72 |
| 2 and 12 | 12 |
| 36 and 48 | 144 |
| 30 and 45 | 90 |
| 8 and 16 | 16 |
| 24 and 40 | 120 |
| 30 and 40 | 120 |
| 8 and 18 | 72 |
| 15 and 35 | 105 |
| 16 and 18 | 144 |
| 2 and 10 | 10 |
| 21 and 28 | 84 |
| 7 and 21 | 21 |
| 18 and 20 | 180 |
| 4 and 18 | 36 |
| 7 and 10 | 70 |
| 12 and 24 | 24 |
| 20 and 25 | 100 |
| 4,5 and 6 | 60 |
| 12 and 28 | 84 |
| 9 and 18 | 18 |
| 14 and 35 | 70 |
| 9 and 11 | 99 |
| 15 and 4 | 60 |
| 12 and 21 | 84 |
| 8 and 11 | 88 |
| 6 and 24 | 24 |
| 6 and 9 | 18 |
| 18 and 45 | 90 |
| 40 and 50 | 200 |
| 10 and 20 | 20 |
| 25 and 30 | 150 |
| 15 and 30 | 30 |
| 27 and 45 | 135 |
| 12 and 36 | 36 |
| 8 and 24 | 24 |
| 32 and 48 | 96 |
| 25 and 35 | 175 |
| 6 and 20 | 60 |
| 28 and 42 | 84 |
| 18 and 36 | 36 |
| 9 and 16 | 144 |
| 14 and 16 | 112 |
| 3 and 15 | 15 |
| 30 and 50 | 150 |
| 18 and 21 | 126 |
| 14 and 18 | 126 |
| 10 and 18 | 90 |
| 2,3 and 7 | 42 |
| 14 and 24 | 168 |
| 12 and 40 | 120 |
| 3 and 6 | 6 |
| 1 and 5 | 5 |
| 4,5 and 6 | 60 |
| 45 and 60 | 180 |
| 15 and 24 | 120 |
| 20 and 50 | 100 |
| 50 and 75 | 150 |
| 3,4 and 5 | 60 |
| 30 and 42 | 210 |
| 7 and 14 | 98 |
| 3,5 and 7 | 105 |
| 4 and 20 | 20 |
| 7 and 13 | 91 |
| 5,6 and 7 | 210 |
| 8 and 32 | 32 |
| 8 and 28 | 56 |
| 30 and 36 | 180 |
| 2,3 and 4 | 12 |
| 6,8 and 12 | 24 |
| 8,10 and 12 | 120 |
| 25 and 40 | 200 |
| 4,6 and 8 | 24 |
| 32 and 40 | 180 |
| 16 and 40 | 80 |
| 21 and 35 | 105 |
| 14 and 28 | 28 |
| 9 and 27 | 27 |
| 12 and 13 | 156 |
| 2 and 8 | 8 |
| 5 and 6 | 30 |
| 12 and 16 | 48 |
Frequently Asked Questions on LCM.
Least common multiple of any group of numbers is defined as the smallest number that will be the multiple of all the numbers in a group.
GCF is Greater Common Factor and LCM is Least Common Multiple.
Commutative Property : LCM(a,b) = LCM(b,a)
Associative Property : LCM(a , LCM(b,c)) = LCM(LCM(a,b),c)
