You can input a number and find the prime factor, factor and factor pair.
Prime Factorization: 2 * 2 * 3
Factors: 1, 2, 3, 4, 6, 12
Factor Pairs : (1,12),(2,6),(3,4)
What is Prime Factorization?

Prime factorization is the method for finding prime factors of a composite number. There is a theorem that states: Any integer greater than one can be uniquely written as product of prime numbers.
Prime factor example
Let's take 6. It can be written as 2 x 3 which is nothing but the multiplication of two prime numbers.
find the prime factorization for 124. 124 = 2 * 2 * 31 , Here all the three factors are prime and the prime factorization of 124 is 22 x 31
How to Factorize a number?

Step 1: As we discussed about integers, we clearly notice that all integers can be written as Multiplication of two numbers. Even we can write prime number in this way.(1 x prime.no).
Step 2: Lets take a number xy.Try to write in multiplication of two numbers. (i.e) x * y.
Step 3: Next is to check whether the number x and y can be written as multiplication of two numbers.We need to repeat this step until the number reaches to prime number.
Example: Factorization of 36
Step 1: Express it as multiplication of two number. 36 = 12 x 3
Step 2: We can write 12 as multiplication of two numbers, 12 = 4 x 3 , 12 = 6 x 2.
Step 3: 4 and 6 can be written as 2 x 2 and 2 x 3 respectively.
Now collect the numbers and we can ignore the duplicate numbers. So now the factors of 12 are >2, 3, 4, 6
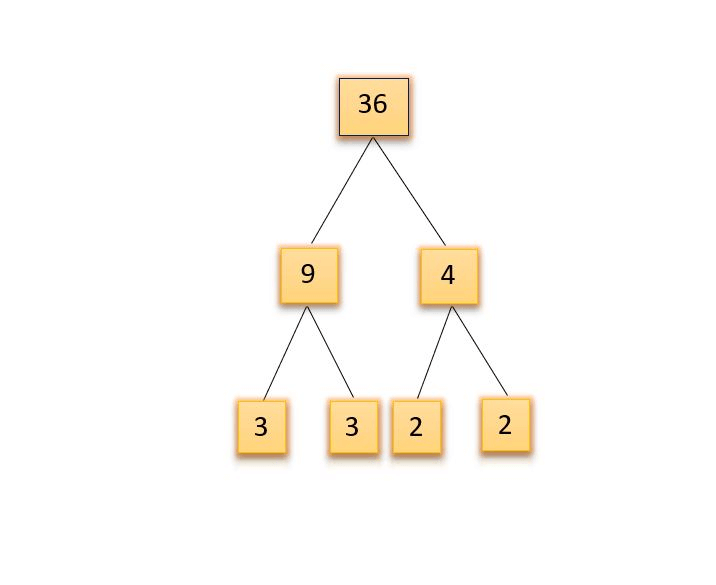
Factor Tree

What is Factor tree? Factor tree is an another way of finding the prime factors of a given number. In this method, we split the given number into two branches and again split the numbers in the branches to two numbers. Repeat this process , until the split number is a prime.
Factor tree of 36 is 2x2 x 3x3 First we split 36 into 9 x 4. And in each branch we have composite so our aim is to split all branch element to multiples of prime numbers.So split 9 as 3 x 3 and 4 as 2 x 2 respectively in the branch. Now at the end node all the numbers are prime numbers.So the factorization of 36 is 2 x 2 3 x 3.
Factorization table

| Factorization of Number | Factors |
|---|---|
| 4 | 1,2,4 |
| 6 | 1,2,3,6 |
| 8 | 1,2,4,8 |
| 9 | 1,3,9 |
| 10 | 1,2,5 |
| 12 | 1,2,3,4,6,12 |
| 14 | 1,2,7,14 |
| 15 | 1,3,5,15 |
| 16 | 1,2,4,8,16 |
| 18 | 1,2,3,6,9,18 |
| 20 | 1,2,4,5,10,20 |
| 21 | 1,3,7,21 |
| 22 | 1,2,11,22 |
| 24 | 1,2,3,4,6,8,12,24 |
| 25 | 1,2,5,25 |
| 26 | 1,2,13,26 |
| 27 | 1,3,9,27 |
| 28 | 1,2,4,7,14,28 |
| 30 | 1,2,3,5,6,10,15,30 |
| 32 | 1,2,4,8,16,32 |
| 33 | 1,3,11,33 |
| 35 | 1,5,7,35 |
| 36 | 1,2,3,4,6,9,12,36 |
| 38 | 1,2,19,38 |
| 40 | 1,2,4,5,8,10,20,40 |
| 42 | 1,2,6,7,21,42 |
| 44 | 1,2,4,11,22,44 |
| 45 | 1,3,5,9,15,45 |
| 48 | 1,2,3,4,6,8,12,16,48 |
| 49 | 1,7,49 |
| 50 | 1,2,5,10,25,50 |
| 51 | 1,3,17,51 |
| 52 | 1,2,4,13,26,52 |
| 54 | 1,2,3,6,9,27,54 |
| 55 | 1,5,11,55 |
| 56 | 1,2,4,7,8,14,28,56 |
| 60 | 1,2,3,4,5,6,10,12,15,20,30,60 |
| 63 | 1,3,7,9 |
| 64 | 1,2,4,8,32,64 |
| 65 | 1,5,13,65 |
| 66 | 1,2,3,6,11,22,33,66 |
| 68 | 1,2,4,7,17,34,64 |
| 70 | 1,2,5,7,10,70 |
| 72 | 1,2,3,4,6,8,12,18,36,72 |
| 75 | 1,3,5,15,25,75 |
| 76 | 1,2,4,19,38,76 |
| 77 | 1,7,11,77 |
| 80 | 1,2,4,5,8,10,16,20,40,80 |
| 81 | 1,3,9,27,81 |
| 84 | 1,2,3,4,6,7,12,21,42,84 |
| 85 | 1,5,17,85 |
| 88 | 1,2,4,8,11,22,44,88 |
| 90 | 1,2,3,5,6,9,15,30,45,90 |
| 91 | 1,7,13,91 |
| 96 | 1,2,3,4,6,8,12,16,24,32,48,96 |
| 98 | 1,2,7,14,49,98 |
| 99 | 1,3,9,11,33,99 |
| 100 | 1,2,4,5,10,20,25.50,100 |
| 105 | 1,3,5,7,15,21,35,105 |
| 108 | 1,2,3,4,6,9,12,18,27,36,54,108 |
| 110 | 1,2,5,10,11,22,55,110 |
| 112 | 1,2,4,7,8,14,16,28,56,112 |
| 120 | 1,2,3,4,5,6,8,10,12,15,20,24,30,40,60,120 |
| 125 | 1,5,25,125 |
| 128 | 1,2,4,8,16,32,64,128 |
| 140 | 1,2,4,5,7,10,14,20,28,35,70,140 |
| 144 | 1,2,3,4,6,8,9,12,16,18,24,36,48,72,144 |
| 147 | 1,3,7,21,49,147 |
| 150 | 1,2,3,5,6,10,15,25,30,50,75,150 |
| 180 | 1,2,3,4,5,6,9,10,12,15,18,20,30,36,45,60,90,180 |
| 196 | 1,2,4,7,14,28,49,98,196 |
| 200 | 1,2,4,5,8,10,20,25,40,50,100,200 |
| 210 | 1,2,3,5,6,7,10,14,15,21,30,35,42,70,105,210 |
| 240 | 1,2,3,4,5,6,8,10,12,15,16,20,24,30,40,48,60,80,120,240 |
| 245 | 1,5,7,35,49,245 |
| 300 | 1,2,3,4,5,6,10,12,15,20,25,30,50,60,75,100,150,300 |
| 360 | 1,2,3,4,5,6,8,9,10,12,15,18,20,24,30,36,40,45,60,72,90,120,180,360 |
Prime Factorization table
| Number | Prime Factors | Prime Factorization |
|---|---|---|
| 4 | 2 | 2 * 2 |
| 6 | 2,3 | 2 * 3 |
| 8 | 2 | 2 * 2 * 2 |
| 9 | 3 | 3 * 3 |
| 10 | 2,5 | 2 * 5 |
| 12 | 2,3 | 2 * 2 * 3 |
| 14 | 2,7 | 2 * 7 |
| 15 | 3,5 | 3 * 5 |
| 16 | 2 | 2 * 2 * 2 * 2 |
| 18 | 2,3 | 2 * 3 * 3 |
| 20 | 2,5 | 2 * 2 * 5 |
| 21 | 3,7 | 3 * 7 |
| 22 | 2,11 | 2 * 11 |
| 24 | 2,3 | 2 * 2 * 2 * 3 |
| 25 | 2,5 | 5 * 5 |
| 26 | 2,13 | 2 * 13 |
| 27 | 3 | 3 * 3 * 3 |
| 28 | 2,7 | 2 * 2 * 7 |
| 30 | 2,3,5 | 2 * 3 * 5 |
| 32 | 2 | 2 * 2 * 2 * 2 * 2 |
| 33 | 3,11 | 3 * 11 |
| 35 | 5,7 | 5 * 7 |
| 36 | 2,3 | 2 * 2 * 3 * 3 |
| 38 | 2,19 | 2 * 19 |
| 40 | 2,5 | 2 * 2 * 2 * 5 |
| 42 | 2,7 | 2 * 3 * 7 |
| 44 | 2,11 | 2 * 2 * 11 |
| 45 | 3,5 | 3 * 3 * 5 |
| 48 | 2,3 | 2 * 2 * 2 * 2 * 3 |
| 49 | 7 | 7 * 7 |
| 50 | 2,5 | 2 * 5 * 5 |
| 51 | 3,17 | 3 * 17 |
| 52 | 2,13 | 2 * 2 * 13 |
| 54 | 2,3 | 2 * 3 * 3 * 3 |
| 55 | 5,11 | 5 * 11 |
| 56 | 2,7 | 2 * 2 * 2 * 7 |
| 60 | 2,3,5 | 2 * 2 * 3 * 5 |
| 63 | 3,7 | 3 * 3 * 7 |
| 64 | 2 | 2 * 2 * 2 * 2 * 2 * 2 |
| 65 | 5,13 | 5 * 13 |
| 66 | 2,3,11 | 2 * 3 * 11 |
| 68 | 2,7 | 2 * 2 * 17 |
| 70 | 2,5,7 | 2 * 5 * 7 |
| 72 | 2,3 | 2 * 2 * 2 * 3 * 3 |
| 75 | 3,5 | 3 * 5 * 5 |
| 76 | 2,19 | 2 * 2 * 19 |
| 77 | 7,11 | 7 * 11 |
| 80 | 2,5 | 2 * 2 * 2 * 2 * 5 |
| 81 | 3 | 3 * 3 * 3 * 3 |
| 84 | 2,3,7 | 2 * 2 * 3 * 7 |
| 85 | 5,17 | 5 * 17 |
| 88 | 2,11 | 2 * 2 * 2 * 11 |
| 90 | 2,3,5 | 2 * 3 * 3 * 5 |
| 91 | 7,13 | 7 * 13 |
| 96 | 2,3 | 2 * 2 * 2 * 2 * 2 * 3 |
| 98 | 2,7 | 2 * 7 * 7 |
| 99 | 3,11 | 3 * 3 * 11 |
| 100 | 2,5 | 2 * 2 * 5 * 5 |
| 105 | 3,5,7 | 3 * 5 * 7 |
| 108 | 2,3 | 2 * 2 * 3 * 3 * 3 |
| 110 | 2,5,11 | 2 * 5 * 11 |
| 112 | 2,7 | 2 * 2 * 2 * 2 * 7 |
| 120 | 2,3,5 | 2 * 2 * 2 * 3 * 5 |
| 125 | 5 | 5 * 5 * 5 |
| 128 | 2 | 2 * 2 * 2 * 2 * 2 * 2 * 2 |
| 140 | 2,5,7 | 2 * 2 * 5 * 7 |
| 144 | 2,3 | 2 * 2 * 2 * 2 * 3 * 3 |
| 147 | 3,7 | 3 * 7 * 7 |
| 150 | 2,3,5 | 2 * 3 * 5 * 5 |
| 180 | 2,3,5 | 2 * 2 * 3 * 3 * 5 |
| 196 | 2,7 | 2 * 2 * 7 * 7 |
| 200 | 2,5 | 2 * 2 * 2 * 5 * 5 |
| 210 | 2,3,5,7 | 2 * 3 * 5 * 7 |
| 240 | 2,3,5 | 2 * 2 * 2 * 2 * 3 * 5 |
| 245 | 5,7 | 5 * 7 * 7 |
| 300 | 2,3,5 | 2 * 2 * 3 * 5 * 5 |
| 360 | 2,3,5 | 2 * 2 * 2 * 3 * 3 * 5 |
Frequently Asked Questions on Prime Factorization

Factorization is the method of breaking the numbers into the factors.
For example: 36 = 4 x 9
Prime factorization is the method of breaking down the numbers to the prime factors.For example: 36 = 22 x 32
Every integer greater can be written as multiplication of prime factors.
There will be many factors for a number.
In that the bigger number is a largest prime factor.
For example : Prime factors of 30 is 2 , 3 and 5.
In the factors list 5 is the biggest one so 5 is the greatest prime factor of 30.
The smallest nunber among all the prime factors of the number is the least / lowest prime factor ?
For example : Prime factors of 30 is 2 , 3 and 5.
In the factors list 2 is the smallest one so 5 is the lowest prime factor of 30.
Factor tree is an another way of finding the prime factors of a given number.
In this method we split the given number into two branches and again splits the numbers in the branches to two numbers.
Repeat this process , untill the splitten number is a prime.
Lets take 30 as an example, 30 can be written as 6 x 5 since 6 is not a prime so split 6 into 2 x 3 .
Now all the three factors are prime. And prime factors of 30 are 2 , 3 , and 5.
Prime factorization of 100:
22 x 52
Factor tree , Long division methods , and Grouping method.