Triangle Calculator Online
Find Missing Angles and Sides of A Triangle. Solve SSS, SAS, SSA using the Triangle Calculator.
You can input in any of the fields and get equivalent values.
 | ||
Result
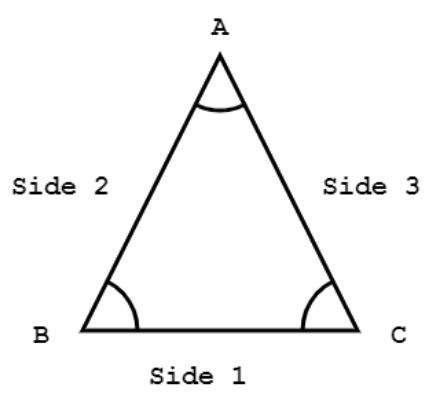
Determine angle of triangle when 3 Sides are given
SSS Method: First use The Law of Cosines to calculate one of the angle
Formula:
cos(A) = (b2 + c2 − a2) / 2bc
Example:
Three sides are 8,6,7
cos(A) = (6 x 6 + 7 x 7 − 8 x 8) / (2×6×7)
A = 75.5°
Again use the Law of Cosines to calculate the second angle
Formula:
cos(B) = (c2 + a2 − b2)/2ca
Example:
cos(B) = (7 x 7 + 8 x 8 − 6 x 6)/(2×7×8)
B = 46.6°
Add the First and second angle,then subtract from 180 to get Third Angle.
Formula:
C = 180° − Angle A° − Angle B°
Example:
C = 180° − 75.5° − 46.6°
C = 57.9°
Calculate Angle when 2 sides and 1 angle is given
SAS Method: First use The Law of Cosines to calculate third side.
Formula:
a2 = b2 + c2 − 2bc cosA
Example:
Two sides are 5,7 and Angle 49°
a2 = 5 x 5 + 7 x 7 - 2 x 5 x 7 x cos(49°)
a = √28.075
a = 5.3
Then use Law of Sines ,find the smaller of other two angles. to calculate the second angle
Formula:
sin B / b = sin A / a
Example:
sin B = (sin(49°) × 5) / 5.29
B = sin-1(0.7122...)
B = 45.4°
Add the First and second angle,then subtract from 180 to get Third Angle.
Formula:
C = 180° − Angle A° − Angle B°
Example:
C = 180° − 49° − 45.4°
C = 85.6°
Calculate Sides when Angle is given
ASA Method: First Calculate the third angle.
Formula:
Angle A+Angle B+Angle C=180°
Example:
Angle A and Angle B are 32° and 47° ,Third Side is 21
32+47+Angle C=180°
Angle C=180-79
Angle C=101°
Then use Law of Sines ,find the smaller of other two angles. to calculate the second angle
Formula:
a/Sin A=b/Sin B=c/Sin C
Example:
a/Sin A=c/Sin C
a(Sin 101)=21(Sin 32)
a=11.34
Repeat the Second step to get the Other side
Formula:
a/Sin A=b/Sin B=c/Sin C
b/Sin B=c/Sin C
Example:
b(Sin 101)=21(Sin 47)
b=15.65
